Cineva, în Africa de Sud, în Pliocen (undeva între Miocen şi Pleistocen), loveşte obsesiv două pietre, fără să pară conştient de ceea ce toată lumea-i ştie: mai are timp, două milioane de ani, să descopere focul. Cosmologii îi dau soarelui nostru încă patru miliarde,  ani de viaţă. De ce ne-am ocupa de soarta Universului?

Câteva repere

“Cosmologie” este numit studiul Universului în ansamblul său, ansamblu care presupune două ingrediente: geometrie şi materie.

Ca să ne fie mai uşor, să ne amintim că geometria din şcoală se face pe hârtie. Putem acolo trasa linii, drepte sau curbe; putem măsura distanţe. Ca şi în spaţiul fizic în care trăim şi în care putem trasa linii (fie şi imaginare) de la un punct la altul şi putem măsura distanţe. Ba chiar şi intervale de timp. Putem face geometrie, exact ca pe foaia de hârtie.

Dacă însă strângem în mână foaia de hârtie? Atunci vedem că interacţiunea dintre spaţiu-timp -foaie de hârtie – şi materie/energie – mână – deformează spaţiu-timpul. Cum anume, depinde de materie şi de modul de interacţiune. În esenţă, o cosmologie înseamnă precizarea geometriei universului (a formei spaţiu-timpului), precizarea componentelor materiei conţinute şi precizarea formei de interacţiune dintre materie şi spaţiu-timp – pe de o parte – şi dintre componentele materiei, pe de altă parte [ 1].

Nu oricum. E nevoie ca din toate acestea să rezulte date specifice, verificabile. E necesar, de exemplu, ca dintr-o astfel de cosmologie să deducem ce procent din Univers înseamnă hidrogen şi ce procent înseamnă carbon; e necesar ca o cosmologie să precizeze şi cum au apărut acestea, ca şi celelalte elemente chimice; e necesar ca o astfel de cosmologie să se potrivească cu ceea ce vedem pe cerul nopţii. Într-un cuvânt, e necesar ca o teorie cosmologică să treacă testul realităţii.

Nu din nimic. Observaţiile care validează o cosmologie sunt şi cele care îi dau naştere. Şi care sunt aceste observaţii?

În primul rând, Universul este în expansiune: foaia de hârtie devine din ce în ce mai mare. Desenele nu. Numai foaia [2].

În al doilea rând, Universul are simetrie maximală. Vom vedea îndată, o bilă este de exemplu maximal simetrică. Bila presupune însă curbură şi aici apare o problemă: curbura universului e aproape zero, în sensul că spaţiu-timpul e aproape plat.

De altfel, în al treilea rând: în oricare punct geometria spaţiu-timpului este plată. Ne putem gândi aici la Pământul nostru: ştim că este curbat. Dar pe suprafeţe mici poate fi considerat plat ca o foaie de hârtie aşa încât, pe distanţe mici, poate fi folosită teorema lui Pitagora.

În fine. Materia observabilă în univers prezintă o structură ciudată, asemănătoare spumei de bărbierit: de departe pare netedă ca o bilă; de aproape are aspect spongios, ca un burete. Spunem că la scară mare Universul este omogen şi izotrop, dar la scară (ceva) mai mică distribuţia materiei este fractală [3,4,5 6]. Cosmologiile obişnuite nu se potrivesc cu acest aspect.

Mai trebuie precizat aici că noţiunea de distanţă este esenţială în orice cosmologie. Aşa cum ştim, distanţa este însă strict legată de poziţie. Diferenţa de poziţie defineşte distanţa aşa cum modul în care definim distanţa diferenţiază geometriile.

Geometrie pe spaţii maximal simetrice

Rămânem, tot ca să ne fie mai uşor, la spaţiu-timpul ca o foaie de hârtie. Din fericire matematica ne ajută aici, limitând numărul spaţiilor maximal simetrice la trei:

- Euclidian, plat. Este foaia de hârtie întinsă pe masă, pe care facem geometria bazată pe axiomele lui Euclid. Nu ne ajută prea mult pentru că nu ia în considerare interacţiunea cu materia: hârtia nu e deformată. Util însă pentru că pe foaia netedă (ştim să) facem geometrie. Ştim cel puţin să definim poziţia unui punct pe foaie utilizând un sistem de coordonate ortonormat (x1, x2) sau, alternativ, un sistem de coordonate polare plane.

- Sferic, pozitiv curbat; presupune un spaţiu închis dar pe care nu putem face geometrie euclidiană: un triunghiu desenat pe o sferă are suma unghiurilor mai mare decât 180⁰ (de unde şi denumirea de pozitiv curbat). Poziţia unui punct într-un astfel de spaţiu este precizată ori prin cele trei coordonate carteziene (x1, x2, x3), ori prin coordonatele sferice .

- Spaţiul hiperbolic, deschis, de curbură negativă: suma unghiurilor este mai mică decât 180⁰. Deschis, aşa cum arată figura alăturată. Poziţia unui punct într-un astfel de spaţiu este precizată, ca şi pentru sferă, prin trei coordonate carteziene sau, echivalent, prin coordonatele sferice .

Cosmologie standard

Este uşor acum să ne imaginăm sfera sau spaţiul hiperbolic dilatându-se într-o expansiune asemănătoare unei bucăţi de tablă încălzite. Dacă am reuşit, deja am înţeles esenţa cosmologiei: spaţiu-timpul se dilată, ca şi cum cândva în trecutul îndepărtat ar fi avut loc o explozie. A tot ce există. Cosmologia standard - în sensul de general acceptată - consideră că Universul a luat naştere printr-o astfel de “explozie”, din nimic (nimicul acela se cheamă câmp Higgs), aşa încât şi astăzi observăm galaxiile gonind prin spaţiu, îndepărtându-se una de alta.
Modelul, gogoneţ şi simpatic, ne înfăţişează un balon care se umflă. Petele de pe balonul de gumă se îndepărtează unele de altele: avem expansiune. Materia conţinută de suprafaţa balonului este cea care determină curbura: avem simetrie şi avem interacţiune dintre materie şi spaţiu-timp.

Explozia iniţială ar fi putut fi o destindere adiabatică şi atunci avem şi formarea structurilor de “spumă”, printr-o tranziţie de fază asemănătoare brânzirii laptelui prea târziu pus la fiert. În linii mari, cosmologia standard reuşeşte să fie cel mai potrivit model [7].
Mai mult, se poate arăta relativ uşor că cele trei spaţii de mai sus se reduc la o singură descriere, cel puţin din punctul nostru de vedere: formal, distanţa dintre două puncte se exprimă la fel, indiferent dacă spaţiul este euclidian, sferic sau hiperbolic.

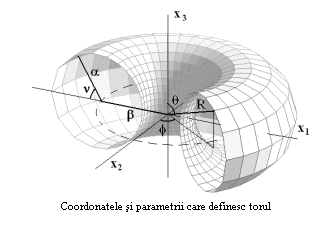
Geometrie pe tor

Să luăm foaia de hârtie şi să o curbăm aşa încât să obţinem un cilindru. Să curbăm cilindrul aşa fel încât să-l aducem la forma unui covrig. Am obţinut un tor simplu.

Definim acum poziţia unui punct pe suprafaţa torului, în sistem cartezian sau, alternativ, în coordonate sferice.

Ecuaţiile sunt:

,

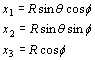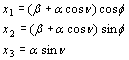
de unde, după puţină algebră, se obţine o ecuaţie de gradul II cu necunoscuta R  simplu de rezolvat.

Cosmologie pe tor

Rezolvând ecuaţia de mai sus, avem soluţiile:

Aceste soluţii conduc la următoarele situaţii:

- Dacă , atunci ,. Prima soluţie relevă starea Universului înainte de a lua naştere: totul se reduce la un punct (�stabilitatea unei astfel de soluţii ne-ar da de gândit). A doua soluţie arată oscilaţii ale universului. Spaţiu-timpul se dilată şi se contractă ciclic, urmând o serie infinită de secvenţe de evoluţie fiecare începând cu o mare explozie (Big Bang) şi încheindu-se cu o implozie (Big Crunch). Curbura este aproape zero peste tot, universul fiind plat cu excepţia momentului exploziei:

- Dacă . Soluţiile (*) devin şi descriu un univers care pulsează cu dublă perioadă:

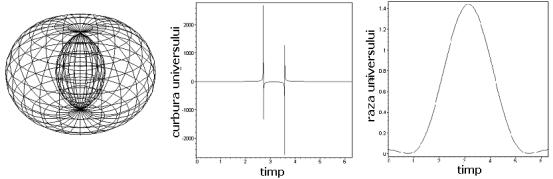
- Pentru , . Avem aici un Univers fără Big Bang, care porneşte în expansiune de la o dimensiune finită şi se contractă fără a ajunge să Ť dispară ť.

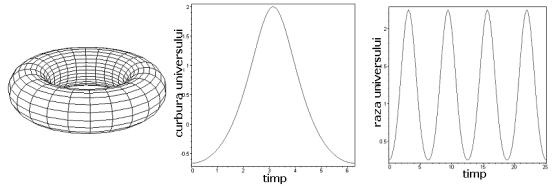
Concluzii

În cuprinsul acestei lucrări am arătat că se poate discuta cosmologie, foarte modernă, într-un mod foarte simplu. Un obişnuit feed-back poate chiar avea loc: ce obţinem dacă în cazul facem ?

Forum: Comentarii pe marginea articolului se pot face in forumul de discutii al site-ului nostru.

Bibliografie:

[1] G.F.R. Ellis, H.vanElst, Cosmological models, Cargese Lectures, 1998

[2] Tamara Davis, UNSW, Lucrare de doctorat,

http://www.mso.anu.edu.au/~tamarad/papers/Davis_Lineweaver_04.pdf

[3] J. Einasto, in “Astronomy, Cosmology and Fundamental Physics”, Proc. Of the 3^rd ESO-CERN Symposium, Dortrecht, Kluwer, pg. 231

[4] J.R. G, S. Mao, C. Park, O. Lahav, The Topology of Large-Scale Structure, Ap. J. 385, 26-31 (1992)

[5] L. Guzzo, A. Iovino, G. Chincarini, R. Giovanelli, M.P.Haynes, Scale-Invariant Clustering in the Large-Scale Distribution of Galaxies, Ap. J., 382 L5 (1991)

[6] P.H. Coleman, L. Pietronero, Phys. Rep., 231, 311 (1992)

[7] N. Ionescu Pallas, Relativitate generală şi cosmologie, Ed. Ştiinţifică şi Enciclopedică, Bucureşti, 1980